「こんなの解けるわけない！」算数でアーモンド型の面積を求める問題が話題になんG民でも無理かw

1 : 2025/12/28(日) 23:11:24.50 ID:FhXE36utM

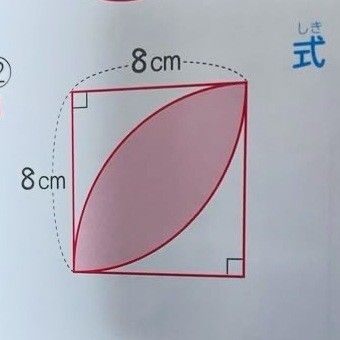
小6の算数の授業で出された図形問題が大人から見ても難易度高い…そんなつぶやきがThreadsに投稿され、話題になっています。

https://news.livedoor.com/article/detail/30279313/

2 : 2025/12/28(日) 23:11:33.07 ID:LJ5WEhsL0

64-2(64-πr^2/4)

=64-2(64-3.14x8x8/4)=36.48

簡単すぎ

6 : 2025/12/28(日) 23:13:50.34 ID:x/rNSOBf0

>>2
はい間違い

13 : 2025/12/28(日) 23:25:00.64 ID:LJ5WEhsL0

>>6
おーーーーーーーいクソガイーーーーーーーーーー

14 : 2025/12/28(日) 23:25:39.03 ID:x/rNSOBf0

>>13
ん？

3 : 2025/12/28(日) 23:11:36.92 ID:FhXE36utM

、

4 : 2025/12/28(日) 23:11:40.32 ID:FhXE36utM

、

5 : 2025/12/28(日) 23:12:55.30 ID:x/rNSOBf0

これわからんってゲェジなんか？

7 : 2025/12/28(日) 23:15:22.18 ID:ffz9A//g0

わかんない
今日中に解けないと明日死ぬかな

8 : 2025/12/28(日) 23:19:18.89 ID:PlHgux9g0

解き方授業で説明したうえにテストに出しますって予習期間与えられて解けないのは流石に何しに学校行ってんのとしか

9 : 2025/12/28(日) 23:19:41.85 ID:kQyIDDyJ0

条件が不明

真円は現行技術で描画できないから解くのは不可能

10 : 2025/12/28(日) 23:21:01.05 ID:Rh50h0cAH

曲線部分が真円の1/4だと決めつけるのは良くない

11 : 2025/12/28(日) 23:21:16.04 ID:xNP9OaPW0

扇型にしてそれの面積も求めてそっから扇型の中の三角形の面積を引いて×2が正解か？
扇型の面積の公式とか全く覚えてねえわ

12 : 2025/12/28(日) 23:22:41.96 ID:x/rNSOBf0

>>11
円の四分の一やろ

19 : 2025/12/28(日) 23:31:37.42 ID:xNP9OaPW0

>>12
あぁ確かに冷静に考えたら円やな
元記事に扇型って書いてあったから扇型って書いちゃったわ

15 : 2025/12/28(日) 23:28:46.41 ID:3g8hAKvS0

なんとなく分かるわ。大人の方の算数力が低いのか？

16 : 2025/12/28(日) 23:29:05.94 ID:J5+rk1g00

(正方形の面積)-(円の面積×1/4)×2で白い部分の面積になるな

17 : 2025/12/28(日) 23:29:25.65 ID:DIV5qn090

メタ推理になるけど赤いところが葉っぱみたいだから8×8にしたんだと思う

18 : 2025/12/28(日) 23:30:25.33 ID:uZzAYy9E0

中受勢ワイはこれは正方形の面積に0.57倍するって覚えてるで
3.14/2-1や

20 : 2025/12/28(日) 23:31:39.53 ID:fCkvbLFH0

小6から見た難易度は知らんけど、オトナから見て難しいは無いやろ

22 : 2025/12/28(日) 23:32:21.20 ID:x/rNSOBf0

>>20
文系だとMARCHでも分数の割り算出来んとかおるしな

25 : 2025/12/28(日) 23:34:11.81 ID:XiL6VmTA0

>>22
早慶でも半分くらいは数学壊滅的やで

27 : 2025/12/28(日) 23:35:16.41 ID:x/rNSOBf0

>>25
きっと小学生の頃は出来たんやろけど詰め込みの末に抜け落ちたんやろか

23 : 2025/12/28(日) 23:32:22.51 ID:Rh50h0cAH

円の中心が正方形のカドからずれてたら超難問やね

24 : 2025/12/28(日) 23:33:14.97 ID:XiL6VmTA0

中学受験してない（つまり算数は強くない）
高校数学は河合偏差値で60前半
62.5の理系卒

初見で解けたわ

26 : 2025/12/28(日) 23:35:08.32 ID:ywExF02X0

円の面積が出せるなら出せる

28 : 2025/12/28(日) 23:36:16.11 ID:Y0dBjYkU0

64-｛［64-（64π÷4）］✖︎2｝
これやないん？

29 : 2025/12/28(日) 23:37:56.69 ID:GLwbN8X/0

SAPIXのときにやったな
0.56だか0.57面積に掛けるんじゃなかったっけ？

30 : 2025/12/28(日) 23:39:14.87 ID:6Kw6+K/J0

36.48が正解やろ
1/4円の面積はπr2乗で16π
正方形の面積は64
逆方向からそれぞれ1/4円を作ってその重なってる領域の面積を求めるってことは単純に64よりも2つの1／4円つまり1／2円がどれだけ大きいかを求めればいい

だから36.48

33 : 2025/12/28(日) 23:40:22.79 ID:x/rNSOBf0

>>30
何でπを3.14にしてんの？

31 : 2025/12/28(日) 23:39:44.61 ID:3g8hAKvS0

こりゃ予想以上に大人の算数力下がってるのやもしれんな…

35 : 2025/12/28(日) 23:42:25.03 ID:1ZIDnK+I0

ヤフーの記事の方のコメントにあるけど
図形を4つ合わせたら円になる
ヒントはこれだけでいい

39 : 2025/12/28(日) 23:46:39.88 ID:PFz2fZ820

昨日VIPにスレ立ってたやつやな